 |
相關閱讀 |
靜態游戲環境中幾種實用的自動尋路算法
 |
>>> 技術話題—商業文明的嶄新時代 >>> | 簡體 傳統 |
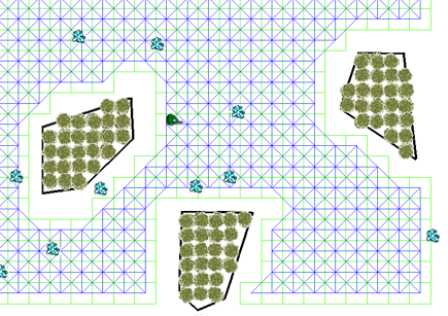
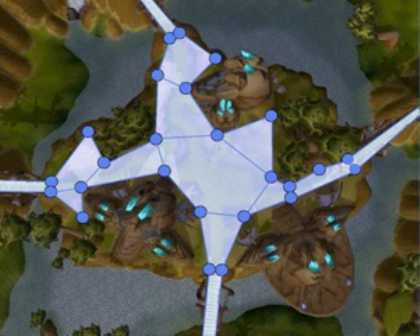
GameRes游資網授權發布 文 / 王凝 這里包括: 我們想使我們的小人從地圖任意一個位置出發,都可以順利避過障礙物到達另一個目的地。這時候該怎么做呢? 有了這些網格,我們只是告訴了小人哪些點是可以走的,但我們還要告訴它在某一個點上有哪些路徑可以選擇。這個很簡單,我們可以選擇某一個點周圍八個點作為可以走的路徑(如果這個方向沒被障礙物擋住的話)。對所有的點重復這一過程,我們就可以生成這個地圖的path networks(路徑網絡)了。如下圖,圖中藍色的線代表路徑網絡。 此時我們就已經完成了對連續的地圖離散化這一過程,小人也就可以在游戲世界里亂走了(注意是亂走~)。這是因為我們還沒有使用搜索算法來告訴小人如何到達目的的,或者說走哪條路可以到達目的地。 在說明常用的搜尋算法之前,我想詳細說明一種游戲中更常用的路徑生成方法,這就是navigation mesh(導航網格)。這里的mesh和grid有區別,mesh可以是很多種形狀的多邊形。下圖中的每一個多邊形都是navigation mesh的組成部分,魔獸世界就用到了這種方法進行地圖的劃分。 請注意這里的劃分出的每一個多邊形都是凸多邊形。這里其實是使用到了凸多變形的性質,在凸多邊形邊上的一個點走到另外一點,不管怎么走都不會走出這個多邊形,如下圖所。相反凹多邊形就不滿足這一性質。 應用到游戲世界里,我們只要在空地上放置凸多邊形,小人在多邊形內怎么走都不會碰到障礙。 我們可以看到,雖然通過這種方法生成的網格相比grid已經大大減少,但是圖上很多相鄰的三角形是可以合并形成新的凸多邊形的。所以我們其實還可以進一步優化,將可以合并成新的凸多邊形的相鄰多邊形合并,并重復這一過程,最終得到下圖。 然后我們可以在每一個網格每一條邊的中點上放置pathnode(路徑點),然后將每一個網格自己邊上的路徑點連接起來就得到了完整的路徑網絡了,如下圖,同上綠色的線代表畫好的navigation mesh,藍色的線代表可以走的路徑網絡。 以上就是navigation mesh的大致思想與方法,其優缺點總結如下: 假設我們已經通過運行Dijkstra和Floyd-Warshall生成了這個navigation table。如果我們需要找到從第0個點到第4的點的最優路徑,我們可以查表上第0行的第4列,列上的數字是1,意思是要從0走到4,第一個要走的點是1;再查第一行第四列,下一個要走的點是3;再查第三行第四列,我們就可以通過3走到目的地4了。這一系列0-1-3-4就是之前計算出的最優路徑。這種方法對于靜態的環境十分有效,只要環境不變,通過提前計算navigation table,在游戲實際運行時只需要O(|V|)的時間復雜度就可以獲得到達目標點的最優路徑了。
想從一個更系統的角度來敘述pathfinding這一系列問題,希望可以成為一個更容易理解的tutorial。這里所涉及的尋路算法不限于RTS這類游戲,其中一些方法可能更適合靜態的游戲環境。
這里所包含的topics涉及:
1、游戲地圖的劃分及其優劣性
Grid (方格)
Navigation Mesh(導航網格)
2、游戲中常用的搜尋算法及其優劣性
A Star search
Dijkstra’s algorithm
Floyd-Warshall algorithm
首先假設我們有下面這樣一個游戲地圖: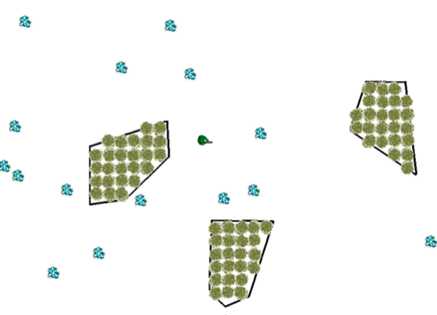
假設我們現在只有一張上面的地圖,這時候小人是不能動的,因為我們需要告訴他哪些地方可以走。由此引入了第一個topic,也就是方格grid。
這個方法很簡單,我只需要選擇一個合適的正方形的邊的大小,然后在地圖上沒有障礙物的地方畫square就可以了。然后我們可以選取每一個square的中心,作為小人實際可以走的點,這樣這個地圖就成了下圖模樣(圖中綠色的方格代表每一個grid,方格的中心才是可以走的點)。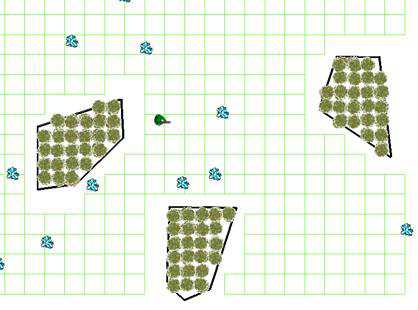
以上就是grid navigation的大致方法了,在此總結一下它的優缺點。
優點:這是一種對地圖離散化的方法。這種方法真的很簡單,非常容易實現而且容易和A star search或者uniform cost search算法結合起來使用。
缺點:使用這種方法劃分出來的網格,小人的移動其實是不連續的。有時可能看起來并不自然,就如下圖所示的情況。而且可以從上圖看出,網格數灰常的多,可能需要大量的資源來計算和存儲路徑。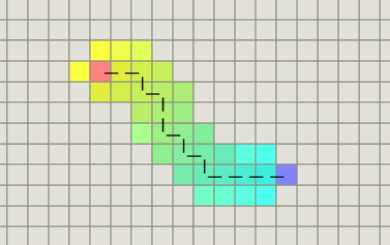
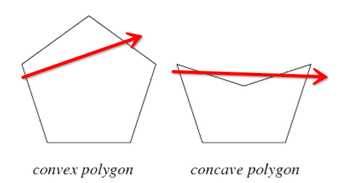
這種方法聽上去挺簡單,實際該怎么操作呢。我們知道任意一個三角形都是凸多邊形,我們可以先通過地圖的邊界點和障礙物的邊界點,將地圖劃分成很多個三角形,如下圖所示。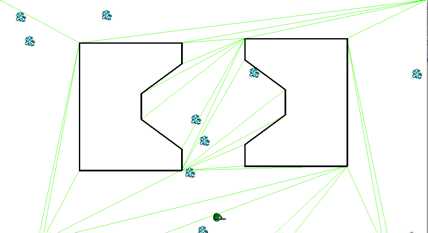
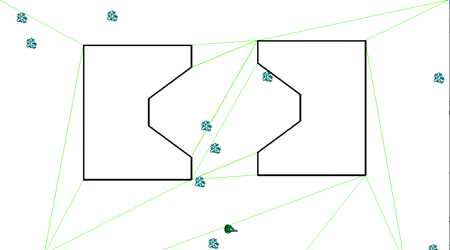
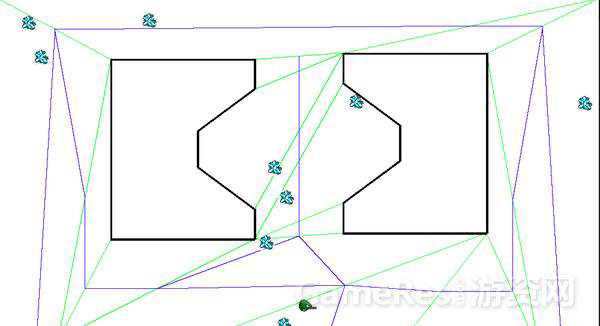
優點:這種方法可以大大減少路徑點和搜尋所需的計算量,同時也使小人的移動更加自然。在這樣的路徑點之間行走,我們其實可以完全無視地圖上的任何障礙物。
缺點:計算三角形和合并相鄰的凸多邊形需要很大的計算量,而且實現起來沒有看上去那么簡單。不過成熟的游戲引擎一般是有現成的解決方案的。
在有了path network(路徑網絡)后,我們就可以開始考慮如果讓小人從一點走到另外一點,如果尋找最優路線了(即返回一系列路徑點)。
首先大多數人會想到A* search。A*是一種非常經典的搜索算法,使用到了heuristic和accumulated cost,細節這里就不贅述了。值得注意的是,這里的heuristic一般是admissible的,也就是說在A*中我們對目標的估計必須小于或等于其實際值,不然可能會出現找不到最優路徑或者根本找不到路徑的情況。當然也有很多情況下我們根本不需要找到最優路徑,只要player覺得合理,who cares optimality呢lol~
這里除去A*的實現細節,我想說明的是,A*是一種single source single destination的算法,它的時間復雜度是O(|E|), E是地圖上所有路徑點所形成的路徑網絡的edge的數目。也就是說A*可以用來計算從一個點到另外一個點的最優路徑。這也就說明A*適合用來對動態環境進行路徑計算,可以實時根據當時的環境立即計算出路徑。相對應的,Dijkstra’s algorithm和Floyd-Warshall適合對于不變的環境來進行計算,下面會說明為什么。
這里介紹的第二種尋路算法就是Dijkstra’s algorithm。說Dijkstra是A*的無heuristic版本,其實并不準確。A*去掉heuristic其實是uniform cost search。而Dijkstra是uniform cost search的multiple destination的變形。也就是說,給出地圖上一個路徑點,使用Dijkstra可以對地圖上所有其他的路徑點一次性計算出最優路徑。Dijkstra的時間復雜度是O(|E|+|V|log|V|),這時E是edge數,V是vertex的數目。從這里可以看出,如果需要對地圖上所有的路徑點同時計算左右路徑,Dijkstra會比使用A*更方便。這也就說明了為什么Dijkstra適合對靜態的環境進行計算,因為靜態的環境是不會變的,我們可以是用Dijkstra對地圖進行preprocess獲得navigation table(后面會說明navigation table如何生成)。我們可以把navigation table記錄下來,這樣在游戲進行的時候從一個路徑點到另外一個路徑點只需要查表就可以了,這樣一來游戲實際運行時的尋路的時間復雜度就減少到了O(V),也就是線性復雜度了,而且對于靜態的環境,我們的navigation table是百分之百可靠的。
另外還想簡要介紹一種尋路算法Floyd-Warshall。這個算法是all sources all destinations的,也就是說給出一個地圖,這個算法可以計算出從所有路徑點到所有其他路徑點的最優路徑,而且可以一邊運行算法一邊生成navigation table,而Dijkstra需要先跑一遍算法,然后從一個路徑點backtrack才能生成navigation table。這個算法的時間復雜度是O(|V|^3。
至于Navigation table, 它大概是長這樣的,假設地圖上已經通過上述的grid或navigation mesh生成了5個路徑點,表示為0到4。表上的數字代表了從某一點要到另外一個點,應該走哪個相臨的點,再從走到的下一個點繼續查表。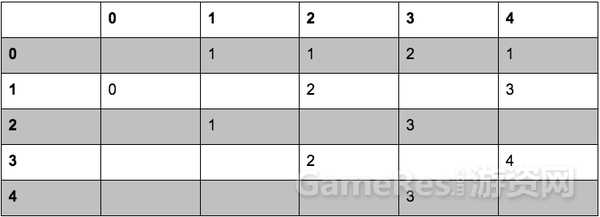
總結:
A* search:single source single destination,速度較快但依賴于heuristic函數的設計。適用于動態環境的尋路,因此適合RTS。
Dijkstra's Algorithm:single souce all destinations,速度也比較快,不需要heuristic函數,但是在建立navigation table的時候需要backtrack。適用于靜態環境的尋路。
Floyd-Warshall Algorithm: all sources all destinations,可以在算法運行過程中建立navigation table。適用于靜態環境的尋路。
對于即時戰略游戲,地圖中所涉及的環境多是動態,所以A*可能更適合一些。
GameRes游資網 王凝 2015-08-23 08:56:55
評論集
暫無評論。
稱謂:
内容:
返回列表

