 |
相關閱讀 |
算算自己有多美——數學美才是真的美!
 |
>>> 民初教育及人才培養 >>> | 簡體 傳統 |
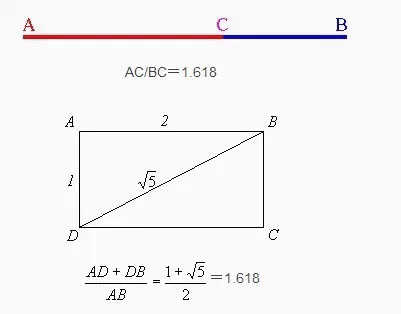
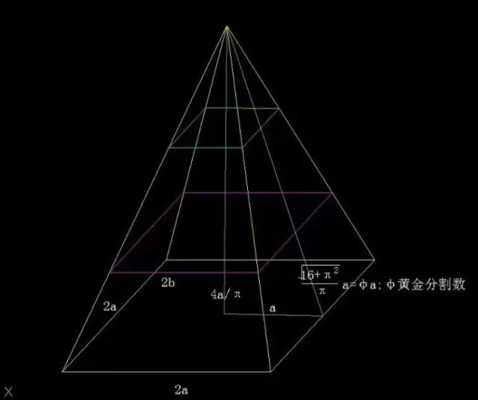
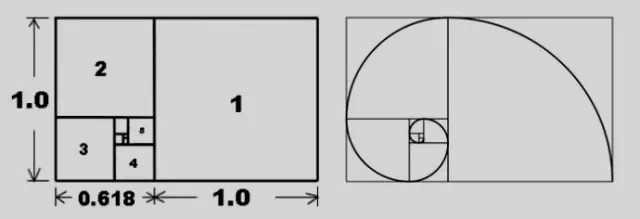
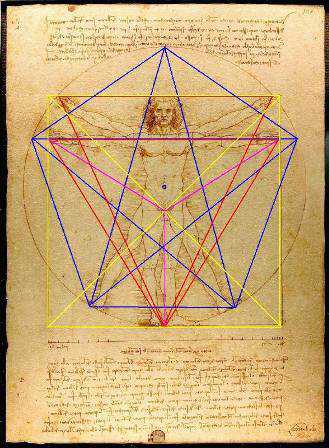
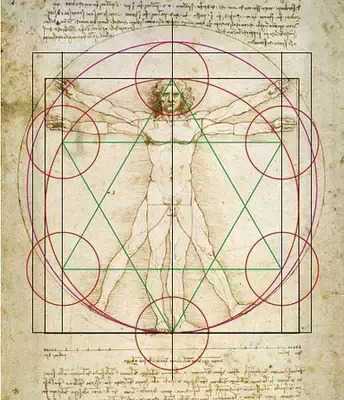
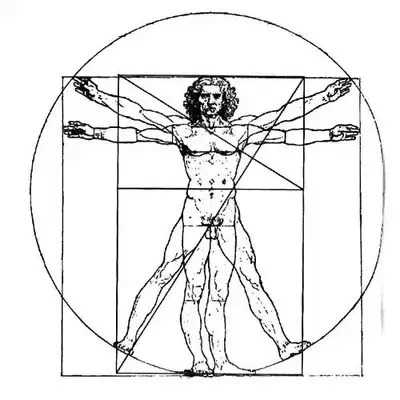
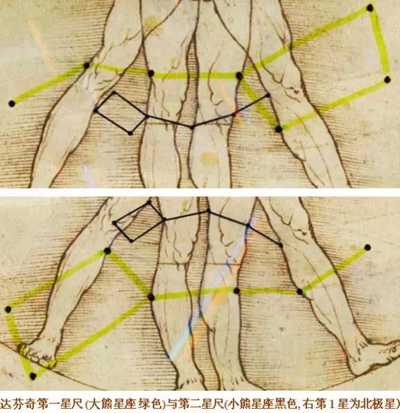
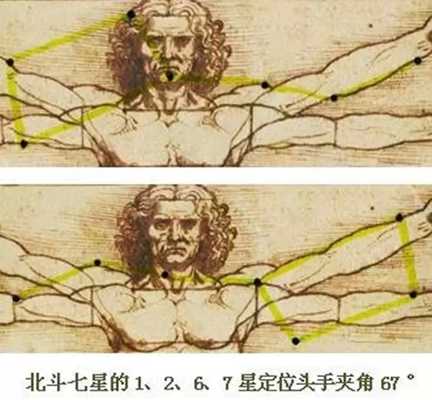
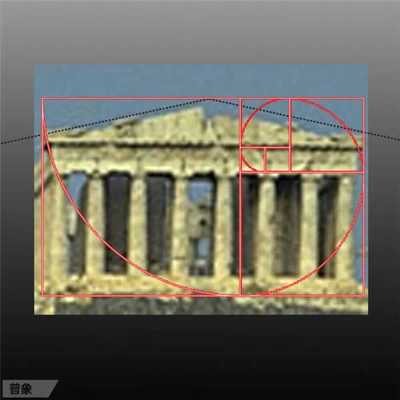
美的量化等式 我們生活的各方面似乎都可以被量化:人的膳食結構(包含熱量,蛋白質,脂肪,碳水化合物,各種維生素,礦物質等等);體型(什么身高對應什么區間的體重);運動(建立有效的鍛煉計劃,實現相應指標)等等。如今,有些可穿戴設備也可以將我們的睡眠量化了,它可以計算出你的深淺度睡眠時間和呼吸頻率。 這讓我想到依靠大數據做出的電視劇《紙牌屋》,從角色安排到劇情發展,迎合觀眾的喜好制作,但是通過計算量化后的作品具有多大魅力?如果美也能被量化,必然就有這個等式: Beauty= b/a= (a+b)/b= 1.618... 相信大家在初中數學課上就學過這個公式了。簡單來講就是把一條線段一分為二,較大部分與較小部分之比等于整體與較大部分之比,其比值約為1∶0.618,即長段為全段的0.618。這個點就是黃金分割點,而0.618也被公認為最具有審美意義的比例數字,1∶0.618是最能引起人的美感的比例。黃金分割數也可以用希臘字母φ(拼音為“phi”,讀作“fee”)表示。 關于黃金分割比例的起源大多認為來自畢達哥拉斯,據說在古希臘,有一天畢達哥拉斯走在街上,在經過鐵匠鋪前他聽到鐵匠打鐵的聲音非常好聽,于是駐足傾聽。他發現鐵匠打鐵節奏很有規律,這個聲音的比例被畢達哥拉斯用數理的方式表達出來,被應用在很多領域。后來很多人專門研究過,開普勒稱其為“神圣分割”,也有人稱其為“金法”。 φ的應用 大自然中,樹葉的葉脈,鸚鵡螺紋都具有黃金分割,這些是大自然作為造物主的杰作。而埃及人建造金字塔也應用了黃金分割,不過這早了畢達哥拉斯1000多年,可見那時候人們已從生活中發現這個奧秘也在應用,只是不明確這個規律。(當然關于金字塔是外星人的發射塔又是一說了。) 由于金字塔經歷了常年的侵蝕,所以以下是理想化模型: 側面傾斜角α,α=51.85°;正方形底面的底邊為2個單位,這樣,正四角錐體的高h,h=1.273;側面的高H,H=1.6188,h≈√H H=1.6188≈Φ(1.618) 側面的高(H)÷底邊的1/2=1.6188÷[2x1/2]=1.6188≈Φ(1.618) 側面的面積=1/2x2xH=1.6188 以正四角錐體的高h為邊長的正四方形面積S,S=h2=1.620 即 1^2+h^2≈Φ^2(學好數理化,走遍天下都不怕!) 既然是美的等式 當然要用藝術品說話 斷臂的維納斯的肚臍 就是黃金分割點 大家不妨琢磨一下自己的肚臍。 重點來了! 矮個子女生根據這個可以算出 你應該穿多高的恨天高 才是黃金比例,才好看啊! 泰姬陵的正面 可以說把黃金分割用到了極致 帕特農神廟 也是建筑中運用黃金分割的典例 《最后的晚餐》中后墻和窗戶 還有前景的桌子和弟子的腳 都存在著黃金分割 《蒙娜麗莎的微笑》 這樣分析也是絕了 《維特魯斯人》 畫名是根據古羅馬杰出的 建筑家維特魯威(Vitruvii)的 名字取的 該建筑家在他的著作《建筑十書》中 曾盛贊人體比例和黃金分割 “維特魯威人”是達芬奇 以比例最精準的男性為藍本 這種“完美比例” 也即是數學上所謂的 “黃金分割” 對于這幅畫,達芬奇自己闡述:建筑師維特魯威斯在他的建筑論文中聲言,他測量人體的方法如下:4指為一掌,4掌為一腳,6掌為一腕尺,4腕尺為一人的身高。4腕尺又為一跨步,24掌為人體總長。兩臂側伸的長度,與身高等同。從發際到下巴的距離,為身高的十分之一。自下巴至腦頂,為身高的八分之一。胸上到發際,為身高的七分之一。乳頭到腦頂,為身高的四分之一。肩寬的最大跨度,是身高的四分之一。臂肘到指根是身高的五分之一,到腋窩夾角是身高的八分之一。手的全長為身高的十分之一。下巴到鼻尖、發際到眉線的距離均與耳長相同,都是臉長的三分之一。 人體中自然的中心點是肚臍。因為如果人把手腳張開,作仰臥姿勢,然后以他的肚臍為中心用圓規畫出一個圓,那么他的手指和腳趾就會與圓周接觸。不僅可以在人體中這樣地畫出圓形,而且可以在人體中畫出方形。即如果由腳底量到頭頂,并把這一量度移到張開的兩手,那么就會發現高和寬相等,恰似平面上用直尺確定方形一樣。 此外,“維特魯斯人”還有這些小秘密哦,只能說列昂納多·達芬奇堪稱藝術與科學巨匠。這里,還要提一個列昂納多:列昂納多·斐波那契。因為以他名字命名的斐波那契數列又稱黃金分割數列,數列如下: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,
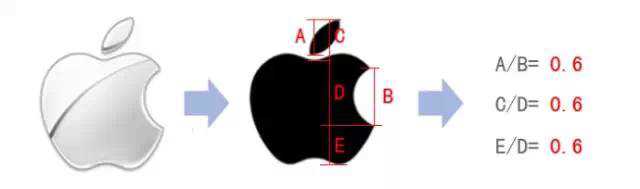
233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368......(特別指出:第0項是0,第1項是第一個1。這個數列從第二項開始,每一項都等于前兩項之和。) 這樣一個完全是自然數的數列,通項公式卻是用無理數來表達的。而且當n趨向于無窮大時,前一項與后一項的比值越來越逼近黃金分割0.618.(或者說后一項與前一項的比值小數部分越來越逼近黃金分割0.618、前一項與后一項的比值越來越逼近黃金分割0.618) 最后,還有一個 喪心病狂的例子 Apple
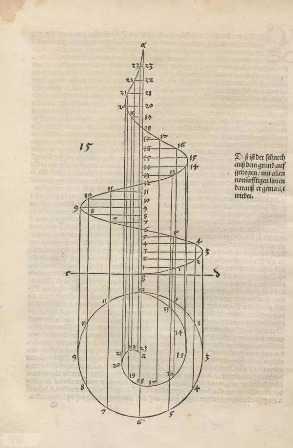
logo蘋果中小葉子的高度和缺口的高度之比是0.6,而缺口的位置也和黃金分割有著千絲萬縷的關系。還有以iphone4為例的主界面圖標,撥號盤,甚至是色彩對比......藝點點們有興趣可以多去發掘。 黃金分割的作用不僅僅體現在諸如繪畫、雕塑、音樂、建筑等藝術領域,而且在管理、工程設計等方面也有著不可忽視的作用。甚至在股市研究,武器設計都有它的身影。當然把比例之美全歸結它是不合理的,盡管物理學家霍金一直在尋找萬物理論:一個統一的,簡單的,優美的公式,但我相信美是絕不應該被量化的。 不過,話又說回來,用理性科學的角度去分析藝術品倒也是蠻有趣的,至少搗鼓了那么久,得出的一些結論還是符合大眾思維和審美習慣的。一個等式可以簡單粗淺地解釋為什么美(符合認知習慣),卻永遠解釋不了什么是美。 以下更多黃金分割經典案例來源于ArtTact 黃金分割其實是一組數列 1,1,2,3,5,8,13,21,34…… 相鄰的兩個數相加得出后一個 無限分裂延伸 沒完沒鳥~~ 請大家留意大衛像、帕特農神廟、蒙娜麗莎、埃及金字塔(內外高&其他各種參數)、墨西哥瑪雅金字塔、DNA、各大星系、各種生物(螺類最明顯),昆蟲的復眼、…… 以下請看圖,不解釋。 這個流派有人信奉有人不信。但是過于迷信這些有理數或者無理數的神奇效果,我覺得是沒啥必要的。用什么工具信奉什么理論不重要,重要的是你做出來的,得是個東西。 其它的也不多說了,我來講一個丟勒 Albrecht Dürer 的故事。 丟勒是文藝復習時期最著名的德國畫家和藝術理論家之一,(我認為他的最高成就在銅版畫和木刻畫)。 他寫過幾何學著作《度量四書》和《人體比例四書》,研究的幾何結構包括螺旋線、蚌線、圓外旋輪線以及三維結構、多面體結構和倍立方,“偏愛托勒密的方法超過了歐幾里德的方法”,非常有前瞻性地把幾何學原理應用到建筑學、工程學和版式編排設計之中。 他曾經說過: 沒有什么東西比一張毫無技巧笨拙的圖片更讓健全的判斷力所討厭了,盡管花費了許多心思和努力。現在這類畫家沒有意識到它們自身錯誤的唯一原因就是,他們沒有學過幾何學。沒有幾何學知識,任何人都不可能是成為一名純粹的藝術家,但是應該譴責他們的老師,他們自己對這種藝術是無知的。——
丟勒 《Of the Just Shaping of letters》 1953 丟勒代表著“健全的判斷力”蔑視你們這些無知的不配稱之為藝術家的小癟三們。是不是很耳熟。 但是,然而, although, but, however,
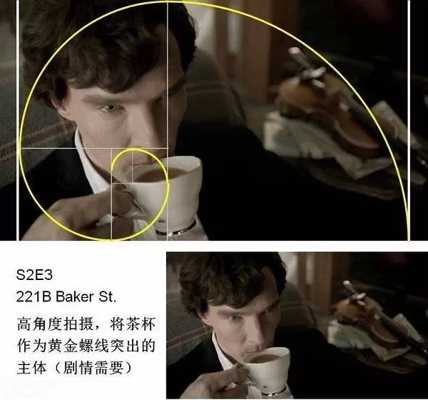
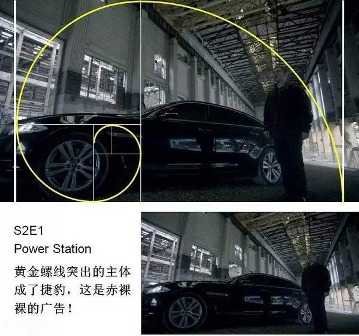
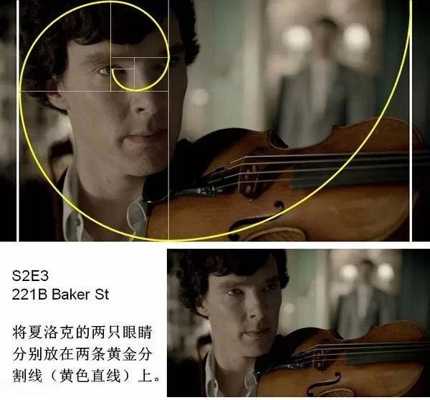
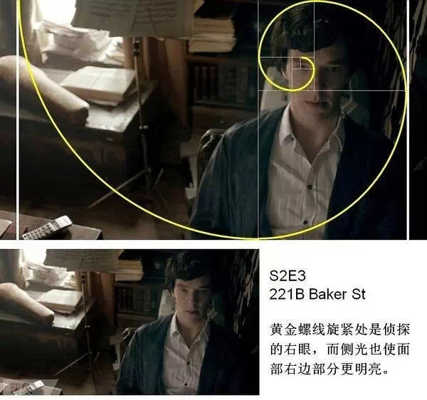
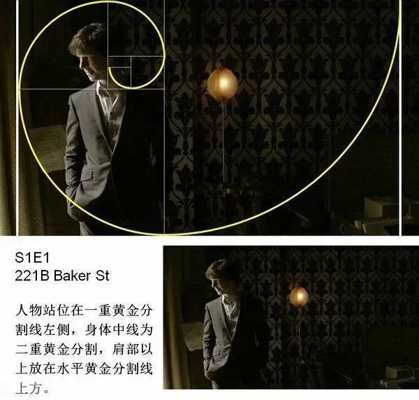
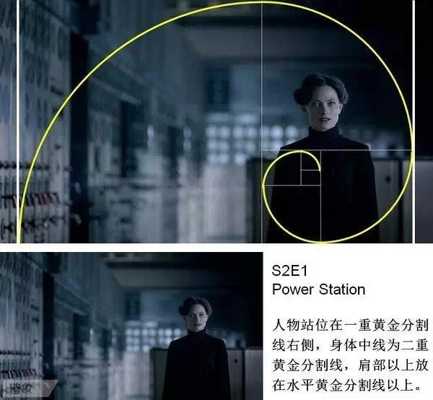
丟勒在死前的一篇附于他的幾何藝術學著作的最后一卷書后的美學短文中,他寫到: 一位藝術家應該憑借豐富的視覺經驗去想象一個美的事物。一個人隨手在半張紙上花一天的時間用鉛筆畫出的東西,或在一塊小木頭上刻出的東西,可能比另一個人花了一年的辛勤勞動炮制出來的大作品更有藝術魅力。 下面,我們用黃金比例來分析《神探夏洛克》畫面構圖: 轉自藝術臺 鳴謝 圖文由公眾號哲學園編輯












base
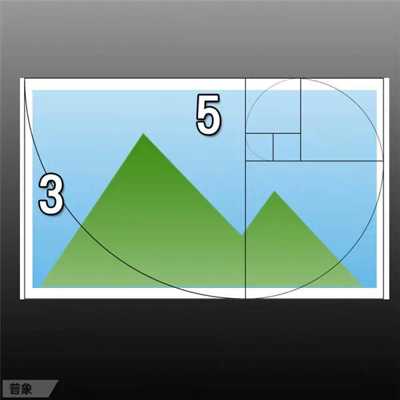
on這組數,我們發現,不僅是藝術,在大自然、宇宙、甚至人體構造中,藝術中也存著的黃金比例。例如:在生命密碼DNA的兩個扭曲螺旋結構組成中我們發現,螺旋之間的寬度和周長比例是0.618,也就是黃金定律,造就了人類潛意識中根深蒂固的審美模式,因此base
on這組數的都被稱為“完美”~~




















文匯教育 2015-08-23 08:54:48
評論集
暫無評論。
稱謂:
内容:
返回列表

