 |
相關閱讀 |
函數構成的世界
 |
>>> 新興科技、社會發展等人文科學探討 >>> | 簡體 傳統 |
計算無處不在。 走進一個機房,在服務器排成的一道道墻之間,聽著風扇的鼓噪,似乎能嗅出0和1在CPU和內存之間不間斷的流動。從算籌算盤,到今天的計算機,我們用作計算的工具終于開始量到質的飛躍。計算機能做的事情越來越多,甚至超越了它們的制造者。上個世紀末,深藍憑借前所未有的搜索和判斷棋局的能力,成為第一臺戰勝人類國際象棋世界冠軍的計算機,但它的勝利仍然仰仗于人類大師賦予的豐富國際象棋知識;而僅僅十余年后,Watson卻已經能憑借自己的算法,先“理解”問題,然后有的放矢地在海量的數據庫中尋找關聯的答案。長此以往,工具將必在更多的方面超越它的制造者。而這一切,都來源于越來越精巧的計算。 計算似乎無所不能,宛如新的上帝。但即使是這位“上帝”,也逃不脫邏輯設定的界限。 第一位發現這一點的,便是圖靈。 《計算的極限》系列 【圖片來自Wikipedia】 丘奇作為圖靈在數學上的前輩,思考的問題自然比圖靈要深遠得多。圖靈考慮的問題,僅僅是希爾伯特的可判定性問題,而丘奇當時思考的,是如何重構數學的基礎。 當時正是第三次數學危機勃發之際,數學界各路人馬對數學基礎應該置于何處爭論不休。當時公理化集合論剛剛建立,作為新事物,自然有人持觀望態度,而丘奇就是其中一位,他覺得自己可以創造一個更好的理論,以此作為數學的基礎。與其選擇集合與包含這兩個概念,他選擇了數學中另一個重要的概念:函數。 數學家眼中的函數,比你想像的要廣泛得多。在中學數學中,說到函數,自然會聯想起它在平面直角坐標系的圖像。這是因為中學數學中的函數,大部分情況下不過是從實數到實數的映射而已。而數學家眼中的函數,可能與程序員眼中的函數更相似:它們更像是一個黑箱,從一邊扔進去某個東西,另一邊就會吐出來另一個東西。 【感謝neko(@iNEKO_mini)提供圖片】 我們并沒有限定能扔進黑箱的東西。事實上,將黑箱本身扔進黑箱也是可以的。對這種把戲,數學家們再熟悉不過了,在泛函分析這一數學分支中,數學家們就經常研究一種叫“算子”的數學概念,在某些特殊情況下,就是那些將一個函數變成另一個函數的函數。所以,不去限定能扔進黑箱的東西,似乎也沒什么問題。 【再次感謝neko(@iNEKO_mini)提供圖片】 總而言之,函數就是將一個函數變成另一個函數的東西。那么,要用符號表達這么普遍的函數概念,我們需要什么呢? 首先,就像在方程中我們用x, y, z等等符號表示未知數,我們也希望能用符號表示未知函數。我們將這些表示未知函數的符號稱為變量。 其次,如果我們手上有兩個函數M和N,那么我們自然希望研究函數N被函數M“處理”之后會變成什么。也就是說,既然M是一個函數,能將一個函數變成另一個函數,那么M會將N這個函數變成什么呢?即使不知道具體的過程,我們也希望能表達最后的結果。所以,我們將N被M處理后得到的結果記為(MN)。這被稱為函數的應用(application)。 最后,也是最抽象的概念,就是函數的抽象(abstraction)。 我們可以用變量x來表示未知的函數,自然也可以用x來構造更多的函數。比如(xx)就表示函數x應用到自己身上的結果,而((xx)y)就表示將剛才得到的結果應用到另一個未知函數y上得到的結果,如此等等,不一而足。如果我們將變量x替換成一個具體的函數f,那么這些包含變量x的表達式就會變成包含具體函數f的表達式。 也就是說,如果我們有一個包含變量x的表達式M,對于任意一個函數f,我們可以將它對應到一個新的表達式,記作M(f),而這個新的表達式是將M中的所有x替換成f所得到的。比如說,如果M=(xx),那么M(f)=(ff),M((yy))=((yy)(yy)),等等。 一個表達式也是一個函數。我們從表達式M出發,可以得到把一個函數f對應到另一個函數M(f)的方法,而這正是一個函數。也就是說,我們能從一個表達式“抽象”出一個函數。我們將這個函數記作λx.M,x是我們所要考慮的自由變量。 【注:在這里,我們只能替換那些所謂的“自由變量”。粗略地說,自由變量是那些之前沒有被抽象過的變量。詳細的技術細節略顯繁復,而且也有辦法繞過,所以于此略過。】 從這三點基本要求出發,丘奇開始定義他的λ演算。他將他考慮的這些函數稱為“λ項”,而所有的λ項都可以從以下三種途徑構造而成: 1. (變量)所有變量x,y,z,…都是λ項。 接下來,丘奇定義了一些λ項之間的轉換法則。 首先是α重命名,這項轉換可以使我們在遵循一定的規則下,任意變換λ項中的變量名稱,而不改變λ項本身的意義。也就是說,λ項中變量的名稱無關緊要,無論是x, y, z還是蘋果、香蕉、榴蓮,又或者是小莊、游游、李清晨,項的本質是不變的。 然后是最重要的β規約: (λx.M)f→βM[x←f] 在這里,M[x←f]實際上是M(f)的嚴謹記法,表明了我們要替換的變量。而β規約實際上就是根據定義計算函數的一個過程。 最后,還有一個η變換。它的實質是所謂的外延性,也就是說,如果兩個項對所有函數的作用都是相同的話,那么就認為這兩個項是相同的。 這么幾條簡單的法則,就是丘奇的λ演算的全部內容。 那么簡單的法則,很難想象λ演算能表達什么復雜的數學概念,這看起來不過是符號的簡單推演而已。但既然同樣簡單的圖靈機中也暗藏玄機,那說不定λ演算也有它自己的復雜內涵。 【圖片來自http://blogs.msdn.com/b/ashleyf】 分崩離析的世界 丘奇最初建立λ演算的目的,是希望將它作為一種邏輯推理的方法。我們可以將某些邏輯公理表達為λ項;對于某個邏輯命題,我們可以先將其轉化為λ項,再根據λ演算的法則將它不斷簡化,而命題正確與否就蘊含在計算結果之中。 通過這種方法,丘奇成功地在λ演算的框架下表達了不少的數學系統。λ演算看起來是如此的成功,甚至達到了無所不能的程度。 但如果我們還記得哥德爾的教訓的話,無所不能有時并不一定是什么好事,因為在數學和邏輯的領域中,對于有意義的邏輯系統,強大的表達能力必然伴隨著堅不可摧的限制。如果一個系統無所不能,那么更大的可能是它本身就自相矛盾。就像一個理論,如果對的也好錯的也罷,正面反面都能解釋得通,那相當于完全沒有解釋。 果然,幾乎在丘奇向學術界展示他的λ演算的同時,克林(Kleene)和科里(Curry)就證明了,作為一個邏輯推理系統,λ演算在本質上就存在著矛盾,它是不一致的。通過適當地構造一些λ項,克林和羅瑟(Rosser)成功地利用λ演算找到了一切命題的證明,甚至包括那些錯誤的命題!一個連錯誤的命題都能證明的邏輯系統,也就是說一個不一致的邏輯系統,沒有任何意義。 值得一提的是,上面這幾位后來都成為了數理邏輯界的大人物。克林和羅瑟是丘奇的學生,而科里則師從希爾伯特。我們后面還會講到這位科里教授,他的事跡之一就是有整整三個不同的編程語言是以他的名字命名的,連中間名都用上了,影響力可見一斑。 事實上,丘奇當初在筑建λ演算之時,就已模糊地認識到了這個問題,但他覺得這只是一種幻象,通過某些適當的限制,就能擺脫這些惱人的問題。但丘奇錯了,實際上這是一個本質性的問題。 那么,問題的根源在何處? 我想,讀過本系列之前文章的讀者應該都猜到了,又是那繞不過去的自我指涉! 自指 但是,自我指涉在什么地方呢? 還記得λ項是什么東西呢?它的原型是函數,但不是一般的函數。在定義λ項之時,我們允許它將任意的λ項轉化為另一個λ項。既然是任意的λ項,那么當然也包括它自己。如果將λ項看成程序的話,那又是一個可以將自己當作輸入數據的程序。與圖靈機不同的是,在λ演算之中,根本沒有數據和程序之分,一切都是λ項,它們既是程序,也是數據。 λ演算的能力不止于此。考慮所謂的Y組合子: Y=λx.(λy.x(yy))(λy.x(yy)) 將它應用到任意一個函數$f$時,我們會得到: Yf=(λx.(λy.x(yy))(λy.x(yy)))f 這樣不停替換下去,得到的結果就相當于將函數$f$應用到自身任意多次。λ演算的能力,特別是在自我指涉方面,于此可見一斑。 正是如此強大的表達能力,使得作為邏輯系統的λ演算一無所能。如果還記得圖靈機是怎么在停機問題上失效的話,實際上利用相似的技巧,對于任意的命題,我們可以構造一個λ演算中的證明,無論命題本身是對是錯。 后來Curry的工作在更深刻的意義上揭示了這一點。他概括了λ演算的某些特性,然后證明了對于無論什么邏輯系統,只要它擁有這些特性,那么它必然是不一致的。而這些特性,也恰好是會礙事的那部分自我指涉所需要的。 于是,作為一個邏輯模型,λ演算一敗涂地。 但丘奇沒有就此止步。雖然λ演算不能如他所愿成為數學的推理基礎,作為一個計算模型似乎倒也不錯。我們可以將一個計算過程看成函數,將輸入數據轉化為輸出數據的函數。于是丘奇將“可有效計算”定義為“可以用λ演算表達的函數”。這時,自我指涉的特性就成為了不可多得的優點,因為這實際上說明λ演算有強大的計算能力。利用自我指涉的特性,通過相似的構造方法,丘奇同樣解決了希爾伯特的可判定性問題,得到了與圖靈相同的結論。 丘奇在構想λ演算之時,瞄準的是更為基本的數學基礎模型,但它卻成為了可計算性的模型,真可謂“無心插柳柳成蔭”。這就是圖靈看到的那篇論文的由來。 不難想象圖靈當時讀到這篇論文時的心情。如果將數學比作攀山,當你千辛萬苦登上一座處女峰,卻驀然發現山頂已經插上了別人的旗幟,你大概會覺得一切都似乎失去了意義。 但數學畢竟不是攀山,不同的路徑可能有不同的景致,要論高下為時尚早。況且要比較兩者,要先知道兩者解決的到底是不是同一個問題。雖然圖靈和丘奇解決的都是同一個問題,但他們對“可計算性”各自做了不同的假定。圖靈認為“可計算的問題”就是圖靈機可以解決的問題,而丘奇則認為那應該是λ演算可以解決的問題。 問題是,圖靈機和λ演算這兩個計算模型,它們解決問題的能力一樣嗎?兩種視點下的可計算性,到底是殊途同歸,還是貌合神離? 來源:科學松鼠會函數構成的世界



2. (應用)如果M和N都是λ項,那么(MN)也是λ項。
3. (抽象)如果M是一個λ項而x是一個變元,那么λx.M也是一個λ項。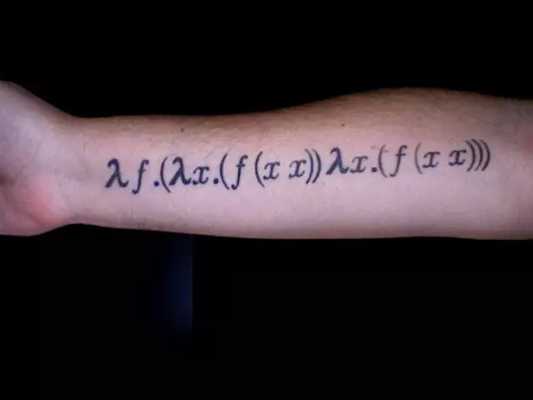
→β(λy.f(yy))(λy.f(yy))
→βf((λy.f(yy))(λy.f(yy)))
=f(Yf)
中科院物理所 2015-08-23 08:48:25
評論集
暫無評論。
稱謂:
内容:
返回列表

